Why is the calculated SLG fault higher than the calculated 3phase fault?

While in most cases it is true that the SLG fault on a bus is lower than the 3Phase fault, there are cases where the SLG fault is higher than 3Phase fault.

This usually occurs when the zero sequence impedance for the fault is less than the positive and negative sequence impedances. This occurs most often when a solidly grounded delta-wye transformer is located nearby.

Figure 1 below is a good example.

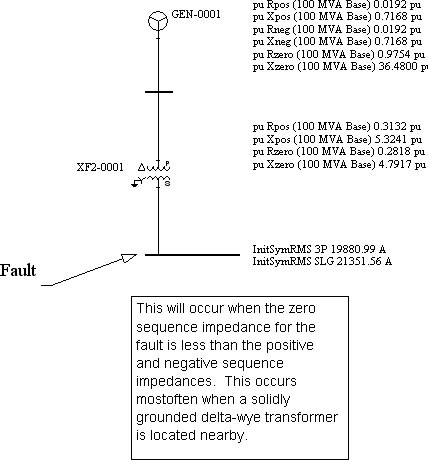
Figure 1

A sample calculation of the sytem above follows below. See also Figure 2.

Given:

Generator:

Size: 15625 KVA 

X"pos = .1120pu   	X/R = 37.4  	Rpos-> = 0.00299pu 

X"neg = .1120pu  	X/R = 37.4    	Rpos-> = 0.00299pu 

X"zero = 5.70pu 		X/R = 37.4  	Rpos-> = 0.1524pu 

Transformer:

Size:  1500 KVA 	13800V/480V  D/YG 

Rpos = .004698 pu 	Xpos = 0.079862pu 

Rneg = .004698 pu   	Xneg = 0.079862pu 

Rzero = .004227pu    	Xzero = 0.071876pu

Converting the impedance to 100MVA we get the following:

Zpunew = Zpuold (Sbasenew/Sbaseold)(Vbaseold/Vbasenew)2

Generator:

X"pos = 0.1120pu(100/15.625)(1.0) = 0.7168pu 	Rpos = 0.00299pu(100/15.625)(1.0) = 0.0192pu

X"neg = 0.1120pu(100/15.625)(1.0) = 0.7168pu  	Rneg = 0.00299pu(100/15.625)(1.0) = 0.0192pu 

X"zero = 5.70pu (100/15.625)(1.0) = 36.48pu  	Rzero = 0.1524pu (100/15.625)(1.0) = 0.9754pu

Transformer:

Rpos = .004698 pu(100/1.5)(1.0) = 0.3132pu 	Xpos = 0.079862pu(100/1.5)(1.0) = 5.3241pu 

Rpos = .004698 pu(100/1.5)(1.0) = 0.3132pu 	Xpos = 0.079862pu(100/1.5)(1.0) = 5.3241 pu 

Rzero = .004227pu(100/1.5)(1.0) = 0.2818pu   	Xzero = 0.071876pu(100/1.5)(1.0) = 4.7917 pu 

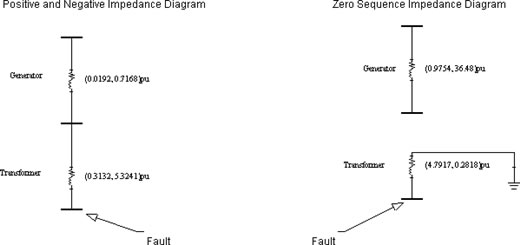
Z+/-thev = (0.0192, 0.7168)pu + (0.3132, 5.3241)pu= (0.3324, 6.0409)pu = (6.05 ë86.85°)pu

Z0thev = (4.7917, 0.2818)pu = (4.799 ë86.63°)pu

Ibase @ 480V

I = S/VÖ3 = 100MVA / 480 Ö3 = 120281.31 A

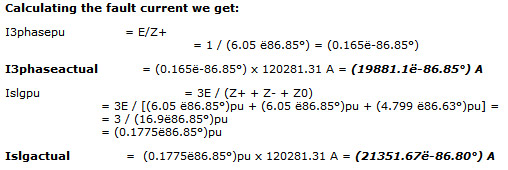
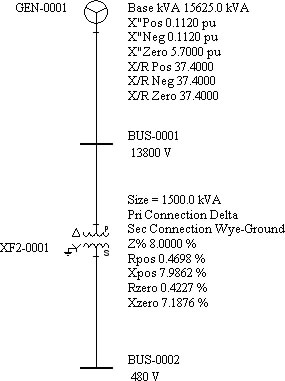
Figure 2