::: SKM Power*Tools ::: ELECTRICAL ENGINEERING SOFTWARE


	3 Winding Transformers

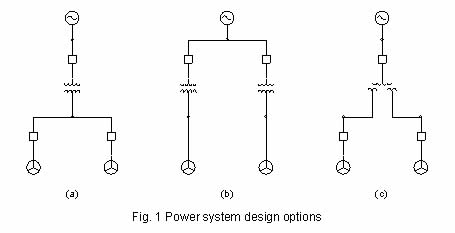
	The information presented in this application guide is for review, approval, interpretation and application by a registered professional engineer only. SKM disclaims any responsibility and liability resulting from the use and interpretation of this information. Reproduction of this material is permitted provided proper acknowledgement is given to SKM Systems Analysis Inc. Introduction At the beginning of a project engineers have many options to choose from when developing the design for the electrical distribution system. For instance consider the case of a new power plant consisting of 2 generators. Three transformation approaches are typically considered to interconnect the generators to the power system. The simplest approach is to serve both generators from a single 2-winding transformer, fig. 1a. This design is typically characterized with the lowest transformation cost but highest available fault duties on the generator bus. The second approach is to supply a single transformer for each generator, fig.1b. This design solves the fault current problem however the transformation costs increase dramatically. Many times to balance cost and fault current issues, engineers select 3-winding transformers, fig. 1c.

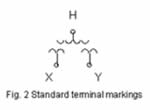
	The term 3-winding transformer can be misleading since a 3-winding transformer may have three or more windings internal to the tank of the transformer. Actually the term 3-winding means a transformer with 3 sets of bushings labeled H for the primary, X for the secondary, and Y for the tertiary, see fig. 2.

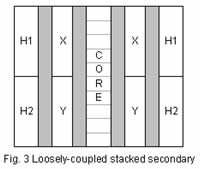
	Impedances are then specified from the H-X, H-Y and X-Y terminals in percent on a chosen winding (typically the X winding) kVA base. The design engineer is responsible for determining the impedances required for the application. The ANSI impedance tolerance for 3-winding transformers is ± 10%, not ± 7½%, for 2-winding transformers. Transformer Winding Configurations Several winding configurations are used in the industry, each with inherent impedance characteristics that engineers must be aware of. The Loosely-Coupled Stacked Secondary (LCSS) design is shown in fig. 3. Notice with this design there are actually four windings around the core. Physically, the H winding is split in two to match the height of the X and Y windings. Electrically, the H1 and H2 windings are configured in parallel inside the tank. This design approach is taken to balance the fields in the H windings when the secondary fields are unbalanced due to an imbalance in load or a fault condition. This design is intended to serve load equally and continuously through the secondary windings. It is not a good design selection if the secondary windings will serve an unbalanced load for an extended period of time, e.g., one secondary breaker open.

	In this case, with equal capacities on both the X and Y windings and impedances expressed on the same base, the following relationships hold.

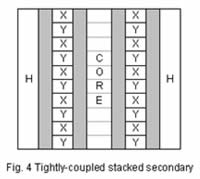
	Another winding configuration is the Tightly-Coupled Stacked Secondary (TCSS) design, see fig. 4. In this case the secondary and tertiary windings are alternately wound around the core. The H-X and H-Y impedances are as previously defined. The X-Y impedance has the following relationship.

	This is not a good design selection in applications where high secondary and tertiary winding fault currents are a concern. This design is more commonly used in traction power and rectifier applications.

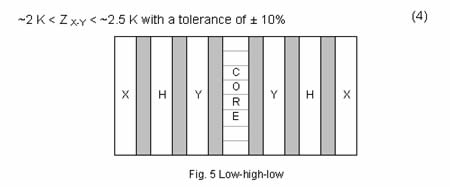
	A third option is the Low-High-Low (LHL) Design shown in fig. 5. Again the H-X and H-Y impedances are as previously defined. The impedance range available from the X-Y windings would be slightly larger than the LCSS design.

	Example 1 Consider a new 480V distribution system that includes 3000kVA of motor load and 600kVA of miscellaneous non-motor load. Assume all motors have an Xd" of 0.15 Ω p.u. The utility service is rated 13.8kV with a short circuit capacity of 600MVA. Investigate the following design configurations.
	• Single 2-winding transformer • Two 2-winding transformers • 3-winding transformer utilizing a LCSS design • 3-winding transformer utilizing a TCSS design • 3-winding transformer utilizing a LHL design
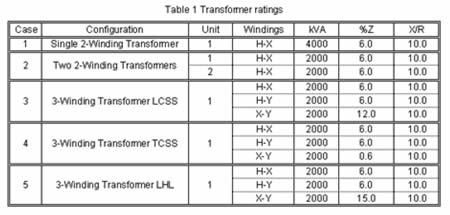
	In this application a total transformer winding capacity of 4000kVA is appropriate. Based on a primary voltage rating of 13.8kV and a standard BIL of 110kV, a typical impedance of 6% is assumed for the application. Table 1 summarizes the transformer ratings selected for each configuration.

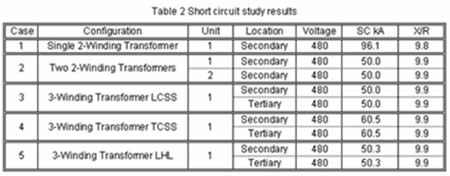
	The results are summarized in Table 2. The initial rationale for considering a 3-winding transformer is confirmed. The single 2-transformer case has the highest fault duties with the lowest transformation cost. The two 2-winding transformer case has the highest transformation cost. A single 3-winding transformer balances both fault current and cost concerns. However, to maintain low fault duties, transformers of the LCSS or LHL design should be utilized.

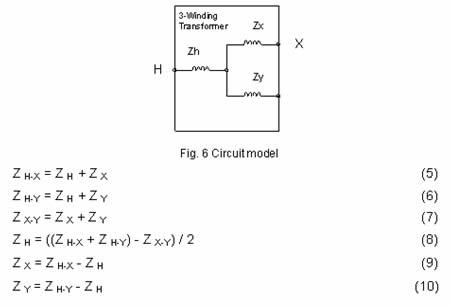
	The results do indicate a peculiar behavior with respect to 3-winding transformers. Note the difference between cases 3 and 5. The secondary-to-tertiary impedance goes up from 12% in case 3 to 15% in case 5, yet the fault duties track opposite. To understand these results a closer inspection of the circuit model is necessary. The 3-winding transformer circuit model consists of 3 impedances connected in star, see fig. 6. Equations 8, 9 and 10 are necessary to convert Z H-X, Z H-Y and Z X-Y impedances to their Z H, Z X and Z Y equivalents.

	The equivalent circuit shown in fig. 6 accurately represents the transformer from a leakage impedance, mutual effects between windings, and load loss standpoint [1]. Exciting currents and no load losses are ignored. Also, please note it is not uncommon for one of the impedances to be negative or zero!

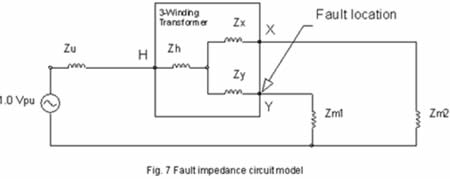
	Example 2 Calculate the winding impedances for Cases 3 and 5 listed in Table 1, and then illustrate the calculation of the available fault current on the tertiary bus, see fig. 7. To simplify the calculations assume all reactance.

	Solution First, convert system impedances to a 2MVA, 480V base.

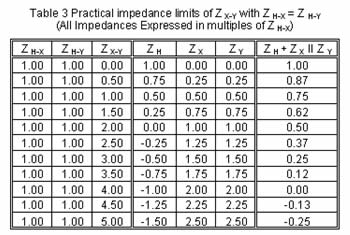
	Z s-t IMPEDANCE LIMITS The TCSS design establishes the lower limit for the secondary-tertiary winding impedance, while the LHL design establishes the upper limit. A theoretical upper limit can be calculated by assuming an infinite bus at the primary of the transformer while shorting the secondary and tertiary terminals (12). Z Thévenin = Z _H + Z _X II Z _Y (12) Again this assumes equal capacities on both the X and Y windings with all impedances expressed on the same base. Impedance limits are summarized in Table 3. The results indicate a maximum upper limit for Z X-Y around 4 times Z H-X. At this point, the Thévenin impedance at the shorted secondary and tertiary terminals approaches zero. Note when Z_X-Y > 4 Z_H-X, the result is an overall negative Thévenin impedance seen outside of the tank of the transformer. This is not possible.

	Example 3 Apply the results listed in this guide to the 3-winding transformer case of example 1, but in this case assume Z H-Y = Z H-X = 6.50% with equal capacities on both the X and Y windings.
	• for Z _X-Y = 0.65% (TCSS) corresponds to a SC kA on the LV terminals of 57.5kA • for Z _X-Y = 13.0% (LCSS) corresponds to a SC kA on the LV terminals of 47.0kA • for Z _X-Y = 16.25% (LHL) corresponds to a SC kA on the LV terminals of 47.3kA • for Z _X-Y = 26.0% corresponds to a SC kA on the LV terminals of 56.2k
	These results illustrate that there is no practical advantage to increasing the secondary-to-tertiary impedance beyond ~2 times the primary-to-secondary impedance. Since higher impedances will only result in higher fault duties and losses.

	References
	• Electrical Transmission and Distribution Reference Book, ABB Power T&D Company, Raleigh, North Carolina, 1997. • Harlow, J.H., Electric Power Transformer Engineering, CRC Press, New York, 2004.
	back to Application guides